设 $f[i][j][0]$ 表示当前金矿向左获利最大值，$f[i][j][1]$ 表示当前金矿向上获利最大值，则有

$$f[i][j][0] = f[i][j-1][0]+a[i]\\ f[i][j][1]=f[i-1][j][1]+b[i] $$

我们还需要将总和求出来。

那么，我们设 $dp[i][j]$ 为 $1 \to i$ 行，$1\to j$ 列的金矿总和最大值，由于只能往左运或往上运，所以可以得出这张图：

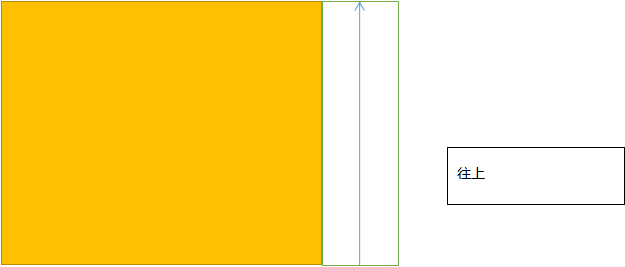
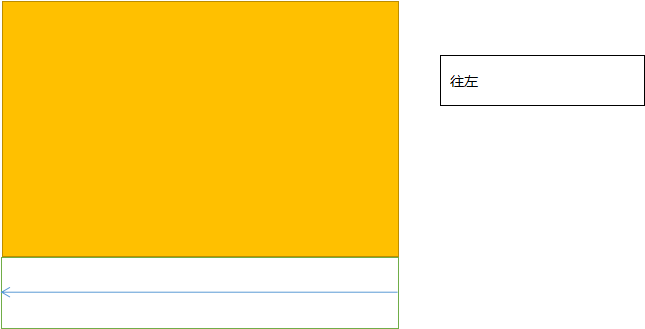
• 往上时，$dp[i][j]=dp[i][j-1]+f[i][j][1]$
• 往左时，$dp[i][j]=dp[i-1][j]+f[i][j][0]$

$$\therefore dp[i][j]=\max(dp[i][j-1]+f[i][j][1],dp[i-1][j]+f[i][j][0]) $$

#include "bits/stdc++.h"
using namespace std;


int f[1500][1500][2];

int dp[1500][1500];
int a[1500][1500];
int b[1500][1500];

int n, m;

int main() {
	freopen ("mine.in", "r", stdin);
	freopen ("mine.out", "w", stdout);
	scanf ("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) scanf ("%d", &a[i][j]);
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) scanf ("%d", &b[i][j]);
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			f[i][j][0] = f[i][j - 1][0] + a[i][j];
			f[i][j][1] = f[i - 1][j][1] + b[i][j];
		}
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			dp[i][j] = max(dp[i - 1][j] + f[i][j][0], dp[i][j - 1] + f[i][j][1]);
		}
	}
	
	printf ("%d", dp[n][m]);
}