3 条题解
-
2
#include<bits/stdc++.h> #define int long long using namespace std; int a[100005],n; signed main(){ freopen("poker.in","r",stdin); freopen("poker.out","w",stdout); cin>>n; for(int i=1;i<=n;i++)cin>>a[i]; int sum=0; for(int i=1;i<=n;i++){ sum+=max(0LL,a[i]-a[i-1]); } cout<<sum; }//5 2 4 1 2 3 -
0
把样例转化成柱状图。

由于只有横向操作,所以一次横涂为一段有牌的区间,为最优解。
暴力时间复杂度为 。
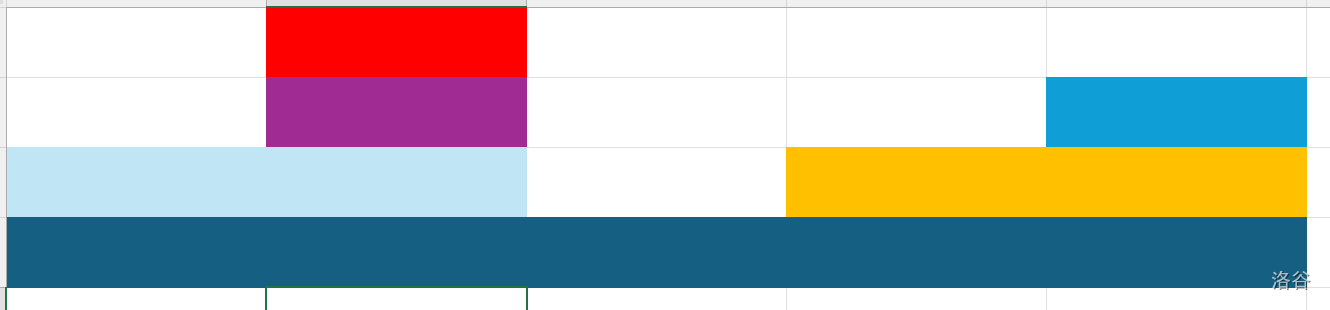
容易发现当 的需要重复刷 ,因为产生间隔。
时间复杂度为 。
可这题大佬提出用线段树。
注意到 。
当 时, 都会有空格,需要多刷,对应区间修改;
查询时只要对于每一个高度查询空格个数累加即可,对应单点查询。
#include <bits/stdc++.h> using namespace std; #define int long long #define up(i,x,y) for(register int i=x;i<=y;++i) using namespace std; inline int read(){int x=0;bool f=0;char ch=getchar();while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}while(isdigit(ch))x=(x<<1)+(x<<3)+(ch^48),ch=getchar();return (f?-x:x);} inline void write(int x){if(x<0)putchar('-'),x=-x;if(x>9)write(x/10);putchar(x%10|48);} inline void writeln(int x){write(x),putchar('\n');} inline void writesp(int x){write(x),putchar(' ');} #define min(a ,b) a < b ? a : b #define max(a ,b) a > b ? a : b const int N = 1e5 + 10; int n ,Q ,a[N]; struct SGT{int l ,r ,sum ,lazy;}tr[N << 2]; inline void pushup(int u){ tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; } inline void pushdown(int u){ if(tr[u].lazy){ tr[u << 1].lazy += tr[u].lazy; tr[u << 1 | 1].lazy += tr[u].lazy; tr[u << 1].sum += (tr[u << 1].r - tr[u << 1].l + 1) * tr[u].lazy; tr[u << 1 | 1].sum += (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1) * tr[u].lazy; tr[u].lazy = 0; } }inline void build(int u,int L,int R){ tr[u].l = L ,tr[u].r = R; if(L == R) return ; int mid = ((L + R) >> 1); build(u << 1 ,L ,mid); build(u << 1 | 1 ,mid + 1, R); pushup(u); } inline void update(int u,int L,int R,int v){ int l = tr[u].l ,r = tr[u].r; if(l >= L && r <= R){ tr[u].sum += (tr[u].r - tr[u].l + 1) * v; tr[u].lazy += v; return; } pushdown(u); int mid = ((l + r) >> 1); if(L <= mid) update(u << 1 ,L ,R ,v); if(mid < R) update(u << 1 | 1, L , R ,v); pushup(u); } inline int query(int u,int L,int R){ int l = tr[u].l ,r = tr[u].r; if(l >= L && r <= R) return tr[u].sum; pushdown(u); int mid = ((l + r) >> 1) ,val = 0; if(L <= mid) val += query(u << 1 ,L , R); if(mid < R) val += query(u << 1 | 1, L ,R); return val; }signed main(){ n = read(); int ans = 0; up(i,1,n) a[i] = read(); build(1 ,1, 100000); up(i,1,n) if (a[i] > a[i - 1]) update (1 ,a[i - 1] + 1 ,a[i] ,1); up(i,1,n) ans += query (1, i, i); writeln (ans); return 0; }
- 1
信息
- ID
- 395
- 时间
- 1000ms
- 内存
- 256MiB
- 难度
- 2
- 标签
- (无)
- 递交数
- 71
- 已通过
- 46
- 上传者
